from the book Trigonometry Surveying and Navigation by G.A. Wentworth, A.M.

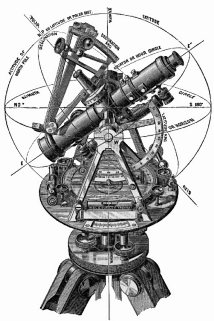
      “Geometry” means, “measuring the earth”; its principles have been used in mapping since ancient times. The simplest geometric figure is the triangle, whose unique properties make it extraordinarily useful. “Triangulation” is the use of triangles for surveying.

      Eratosthenes, a Greek who lived in the 2nd century BC, estimated the earth’s size by comparing the angles of the midsummer sun at two locations. But using the properties of triangles for land surveying did not become common until the 17th century AD.

      Triangles have properties that make them uniquely useful in survey work. First, for any plane triangle, the angles add up to 180 degrees. In addition, the ratio between any angle’s sine and the side opposite that angle is constant for a given triangle. Hindus in the 6th century and Arabs in the 11th century apparently knew about sines and triangles but did not apply them to practical surveying. In 17th-century Europe, triangulation revolutionized mapmaking, producing land measurements far more accurate than earlier estimates.

      The word “sine” comes from the Latin “sinus,” from the Arabic “jayb” meaning “a fold in a garment”, because it measures the amount of curvature of an angle. To understand how a sine is calculated, imagine a clock with one hand on the 1 and another hand on the 3. A line drawn downwards from the 1:00 position will cross the horizontal hand half-way on its length. Thus, an angle of 30 degrees has a sine of ½ or 0.5. From the 2:00 position, or 60 degrees, the sine would be 0.867, and so forth. For any triangle, where A, B, and C are angles, and a, b, and c are the sides opposite those angles, a/sine A = b/sine B = c/sine C. Thus, by finding only two angles and the length of one side, a surveyor can “solve” the triangle by using sines to calculate distances that could not be measured directly.

      To begin triangulation, a 17th-century surveyor laid out an initial triangle by plotting three points: two at the ends of a base line and one at a distant landmark. Using a plane table or theodolite (or a transit like the one pictured above), the surveyor measured the angles towards the landmark at both ends of the base line. The baseline itself was measured by counting revolutions of a wheel or by using measuring chains or rods laid end to end. Once one triangle had been measured, further triangles could be constructed from its sides, producing chains of triangles that could accurately measure long distances. (The earth’s curvature did not cause problems with relatively small triangles.)

      The first practical use of triangulation in mapping a country began in 1668, when Jean Picard and Jean Dominique Cassini, two French astronomers and mathematicians, began the first scientific survey of France. (Cassini was born in Italy but came to France at the behest of the King. As an astronomer he found the gap in Saturn’s rings and timed the transits of the planet’s moons; the space probe presently heading toward Saturn bears his name.) Picard measured a series of triangles between Sourdon and Malvoisine to determine a meridian through Paris, and continued to triangulate distances to the coast. Whether through honest error or national pride, maps to that time had drawn the country larger than life. When Louis XIV saw Picard’s more accurate map of an apparently smaller France, he is said to have remarked, “Your work has cost me a large part of my state!”